【BUUCTF】CRYPTO-刷题记录-RSA
题目描述
解题步骤
下载附件,得到:
1 | 在一次RSA密钥对生成中,假设p=473398607161,q=4511491,e=17 |
p = 473398607161q = 4511491e = 17
要求:
- 计算私钥
d,使得:d ≡ e⁻¹ mod φ(n) - 其中
φ(n) = (p-1)*(q-1) - 最终以
flag{d}形式提交
主要步骤:
- 计算欧拉函数:
φ(n) = (p-1)*(q-1) - 计算
d = e⁻¹ mod φ(n),即d是e在模φ(n)下的模逆元 - 输出
d
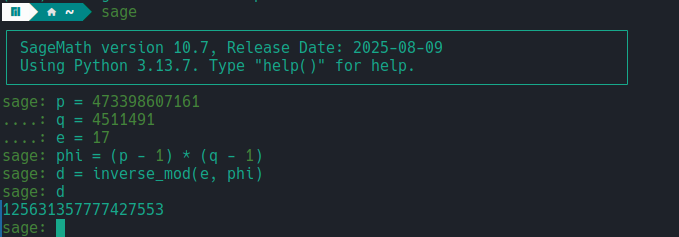
SageMath 是非常适合数论和 RSA 计算的工具,支持大整数和模逆元直接计算。
1 | # RSA 参数 |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 末心的小博客!