【BUUCTF】CRYPTO-刷题记录-变异凯撒
题目描述
解题步骤
下载附件,得到:
1 | 加密密文:afZ_r9VYfScOeO_UL^RWUc |
结合题目,进行分析,其实古典密码还是要看每个字符的关联。
我们根据附件的提示,比如:
1 | 如果不考虑加密密文的倒序、变换 |
那么我们继续想一下:
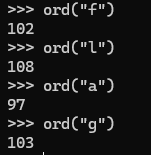
1 | f = 102 |
计算一下前面四位:
1 | f - a = 102 - 97 = 5 |
这下懂了吗?也就是递增去减
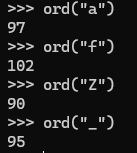
| 明文 | ASCII | 密文 | ASCII | 差值(明文 - 密文) |
|---|---|---|---|---|
| f | 102 | a | 97 | 102 - 97 = 5 |
| l | 108 | f | 102 | 108 - 102 = 6 |
| a | 97 | Z | 90 | 97 - 90 = 7 |
| g | 103 | _ | 95 | 103 - 95 = 8 |
差值是:5, 6, 7, 8 —— 每次递增 1。
也就是说,加密方式是:
密文字符 = 明文字符 - (5 + 位置)
或者说:第 i 个字符(从 0 开始)被减去了 (5 + i)
我们要对密文的每个字符进行逆操作:
明文字符 = 密文字符 + (5 + 位置)
其中位置从 0 开始。
这是一种变种凯撒密码(Caesar Cipher Variant),每个字符的偏移量不是固定的,而是随着位置递增(从5开始)。
本质是:$偏移量 = 5 + index$
1 | # -*- coding: utf-8 -*- |
1 | 密文: afZ_r9VYfScOeO_UL^RWUc |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 末心的小博客!