1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
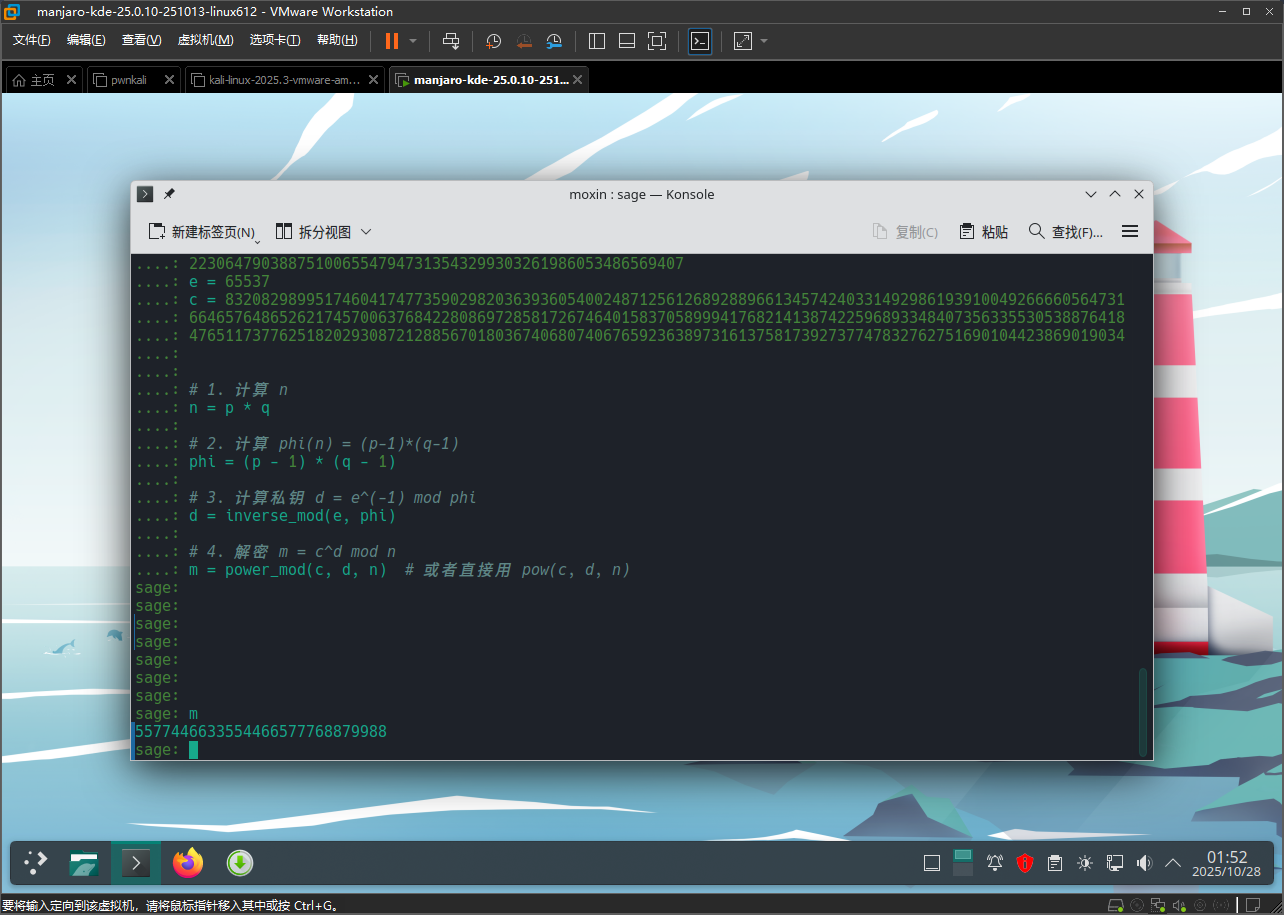
| # RSA 参数
p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e = 65537
c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034
# 1. 计算 n
n = p * q
# 2. 计算 phi(n) = (p-1)*(q-1)
phi = (p - 1) * (q - 1)
# 3. 计算私钥 d = e^(-1) mod phi
d = inverse_mod(e, phi)
# 4. 解密 m = c^d mod n
m = power_mod(c, d, n) # 或者直接用 pow(c, d, n)
|