题目信息

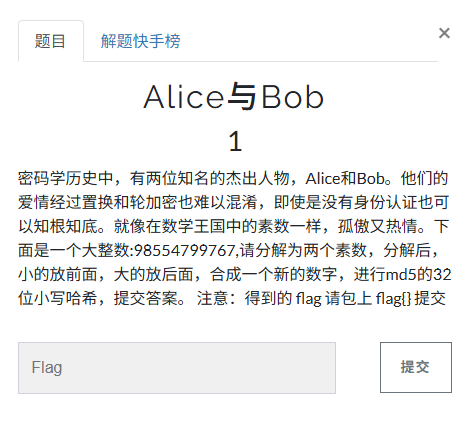
解题步骤

密码学历史中，有两位知名的杰出人物，Alice和Bob。他们的爱情经过置换和轮加密也难以混淆，即使是没有身份认证也可以知根知底。就像在数学王国中的素数一样，孤傲又热情。下面是一个大整数:98554799767,请分解为两个素数，分解后，小的放前面，大的放后面，合成一个新的数字，进行md5的32位小写哈希，提交答案。 注意：得到的 flag 请包上 flag{} 提交

寻找那对“命中注定”的素数

给定的数字是：

1
98554799767

它看起来很大，但在现代计算面前，不过是小菜一碟。

如果这是 RSA 的模数 $n = p \times q$，那么 $p$ 和 $q$ 都是素数，且通常接近 $\sqrt{N}$。

于是我打开 Python，轻声说道：

1
2
3
4
5
import math

N = 98554799767
sqrt_N = int(math.isqrt(N))
print(f"√N ≈ {sqrt_N}")

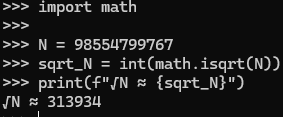
所以，我只需要从 313934 附近开始，向下寻找能整除 N 的素数。

1
2
3
4
5
6
7
p = sqrt_N
while p > 1:
    if N % p == 0:
        q = N // p
        print(f"Found! p = {p}, q = {q}")
        break
    p -= 1

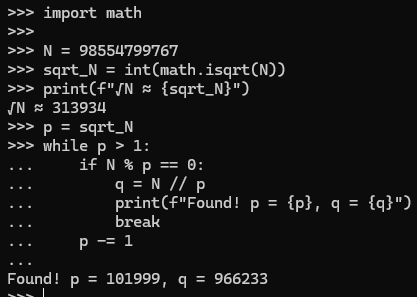
我屏住呼吸——两个都是素数吗？

快速验证：

1
2
3
4
5
6
7
8
9
10
def is_prime(n):
    if n < 2:
        return False
    for i in range(2, int(math.isqrt(n)) + 1):
        if n % i == 0:
            return False
    return True

print(is_prime(101999))  # True
print(is_prime(966233))  # True


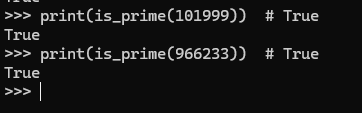
成功！
Alice 是 101999，Bob 是 966233，他们在 98554799767 中重逢。

合成新数字

题目说：“小的放前面，大的放后面”。

所以：
$新数字 = 101999966233$

生成 MD5 哈希

现在，我对这个“相遇之数”进行 MD5 哈希：

1
2
3
4
5
import hashlib

combined = "101999966233"
md5 = hashlib.md5(combined.encode()).hexdigest()
print(md5)

得到：d450209323a847c8d01c6be47c81811a

献给 Alice 和 Bob 的情书

将哈希值包上 flag{}，就是这道题的最终答案：flag{d450209323a847c8d01c6be47c81811a}

素数的爱情哲学

在这个世界里，大多数数字都可以被分解、被预测、被破解。
但素数不同，它们孤傲、不可分割，像极了爱情最初的模样。

而当两个素数相遇，它们的乘积就成了密码学的基石——既公开于世，又守护着彼此的秘密。

就像 Alice 和 Bob，
即使没有身份认证，也能知根知底；
即使历经置换与轮加密，也无法混淆真心。

这道题，不只是数学，
更是一封写给密码学的情书。