题目信息

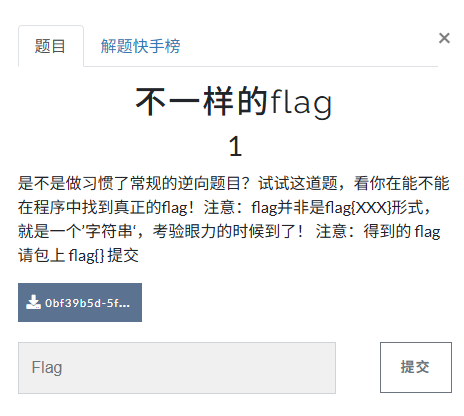
题目信息

解题记录

DIE分析

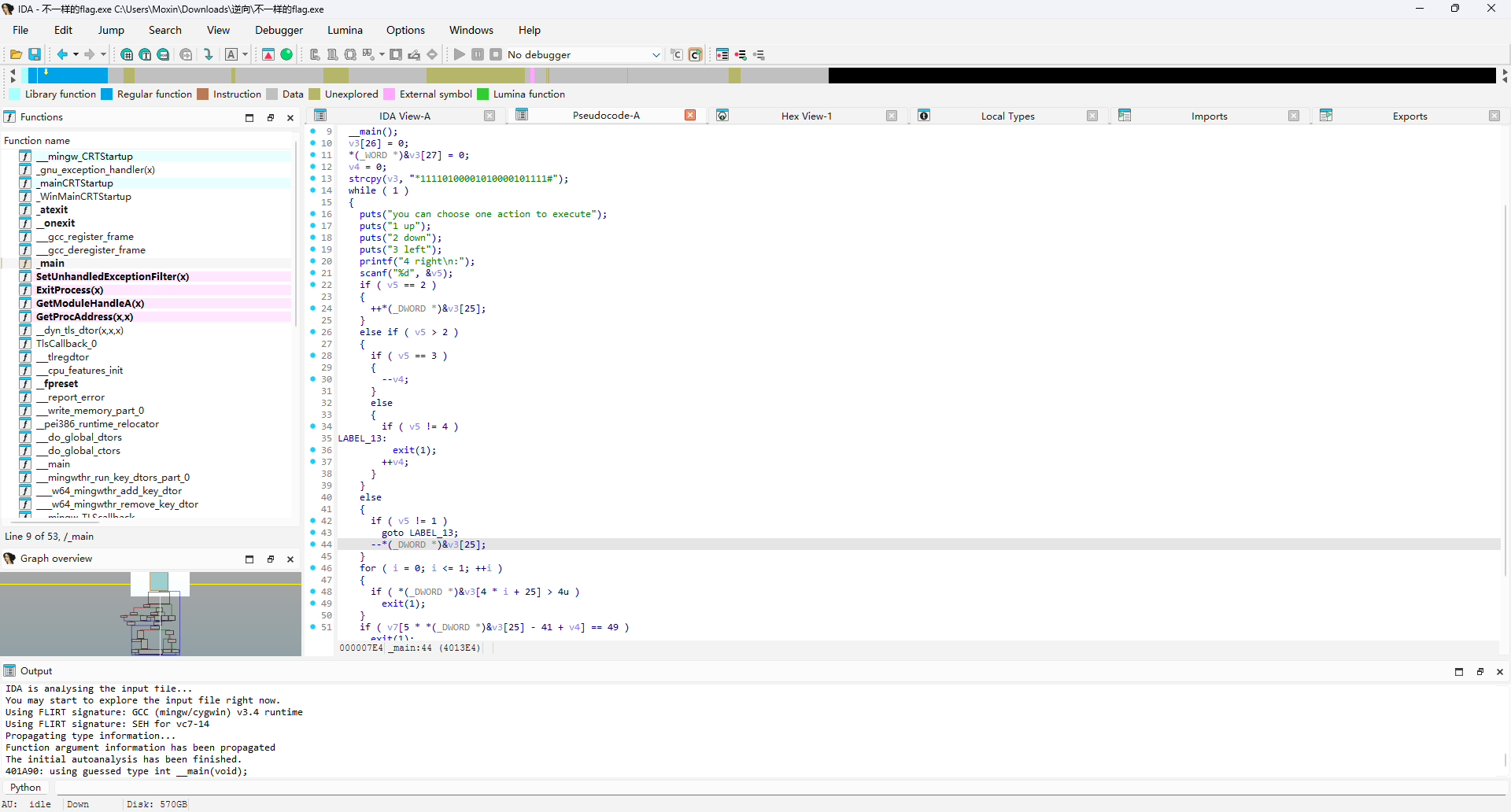
IDA分析

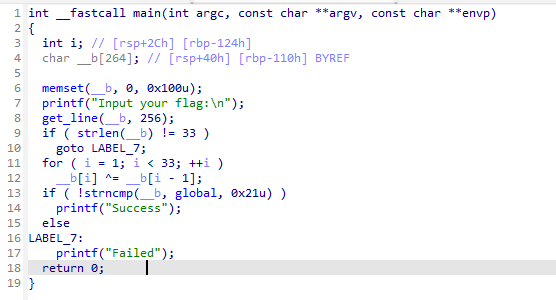
根据提示，发现是个迷宫题目

回到伪代码：

v3 的内容是 “*11110100001010000101111#”，其实也就是地图数据。

1
*1111 01000 01010 00010 111#

共 25 个字符 + 起始 * + 结束 # 。

而在下面判断部分里，有这段关键逻辑：

1
2
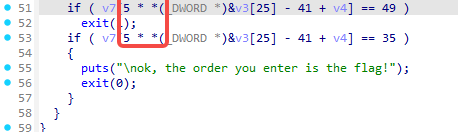
3
if ( v7[5 * *(_DWORD *)&v3[25] - 41 + v4] == 49 )
    exit(1);
if ( v7[5 * *(_DWORD *)&v3[25] - 41 + v4] == 35 )

这里的索引表达式：

1
5 * *(_DWORD *)&v3[25] - 41 + v4

说明：

  • *(_DWORD *)&v3[25] 是纵坐标（即 y）
  • v4 是横坐标（即 x）
  • 每行的偏移是乘以 5

说明地图是 5 列一行，即 5×5 的网格！

5×5 一共 25 个格子，刚好对应字符串里除开起点 * 和终点 # 的 25 个中间字符。

把字符串 *11110100001010000101111# 看作 5×5 的网格（按行优先）

1
2
3
4
5
6
7
8
9
10
(0,0) (0,1) (0,2) (0,3) (0,4)
  *     1     1     1     1
(1,0) (1,1) (1,2) (1,3) (1,4)
  0     1     0     0     0
(2,0) (2,1) (2,2) (2,3) (2,4)
  0     1     0     1     0
(3,0) (3,1) (3,2) (3,3) (3,4)
  0     0     0     1     0
(4,0) (4,1) (4,2) (4,3) (4,4)
  1     1     1     1     #

起点 * 在 (0,0)，目标 # 在 (4,4)。字符 1 表示不可通行（程序会 exit(1)），0/* 可通行。

程序里 1 对应 up（y—），2 对应 down（y++），3 left（x—），4 right（x++）。并有边界检查（坐标必须在 0..4）。

用 BFS（或手工）找出从 (0,0) 到 (4,4) 的一条不经过 1 的最短路径，得到动作序列：

1
down, down, down, right, right, up, up, right, right, down, down, down

对应数字映射就是：

1
2 2 2 4 4 1 1 4 4 2 2 2

flag{222441144222}

BFS（宽度优先搜索）求路径

我们用 BFS 搜索从 *（0,0）到 #（4,4）的最短路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
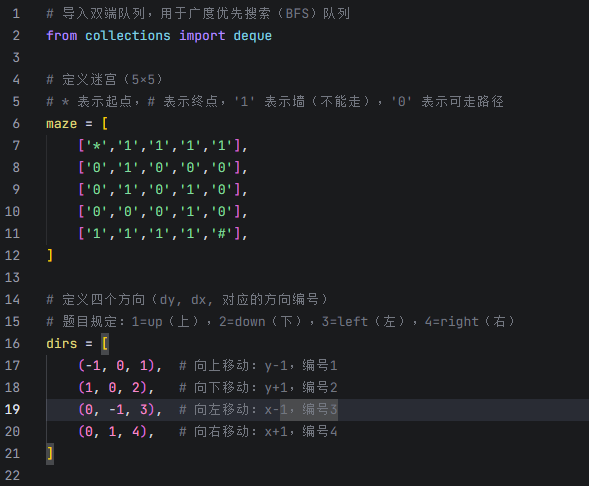
67
# 导入双端队列，用于广度优先搜索（BFS）队列
from collections import deque

# 定义迷宫（5×5）
# * 表示起点，# 表示终点，'1' 表示墙（不能走），'0' 表示可走路径
maze = [
    ['*','1','1','1','1'],
    ['0','1','0','0','0'],
    ['0','1','0','1','0'],
    ['0','0','0','1','0'],
    ['1','1','1','1','#'],
]

# 定义四个方向（dy, dx, 对应的方向编号）
# 题目规定：1=up（上），2=down（下），3=left（左），4=right（右）
dirs = [
    (-1, 0, 1),  # 向上移动：y-1，编号1
    (1, 0, 2),   # 向下移动：y+1，编号2
    (0, -1, 3),  # 向左移动：x-1，编号3
    (0, 1, 4),   # 向右移动：x+1，编号4
]

# 迷宫的大小
n = 5

# 起点坐标（在第0行第0列）
start = (0, 0)

# 终点坐标（在第4行第4列）
goal = (4, 4)

# 初始化 BFS 队列，内容为一个元组：
# ((当前位置坐标), [到达当前位置的动作序列])
# 初始时位置是起点 (0,0)，路径为空列表 []
q = deque([(start, [])])

# 记录访问过的节点，避免重复搜索
visited = {start}

# BFS 主循环：不断从队列中取出一个点，探索它的四个方向
while q:
    # 取出队首元素（当前位置坐标 + 走到这的路径）
    (y, x), path = q.popleft()

    # 打印当前状态（调试用，可以注释掉）
    # print(f"当前坐标=({y},{x})，当前路径={path}")

    # 判断是否到达目标点
    if (y, x) == goal:
        # 找到目标点，输出路径并退出
        print("找到路径：", ''.join(map(str, path)))
        break

    # 遍历四个方向（上、下、左、右）
    for dy, dx, d in dirs:
        ny, nx = y + dy, x + dx  # 计算新坐标
        # 检查是否越界（必须在 0~4 范围内）
        if 0 <= ny < n and 0 <= nx < n and (ny, nx) not in visited:
            # 检查该格是否不是墙（'1' 为墙）
            if maze[ny][nx] != '1':
                # 标记为已访问
                visited.add((ny, nx))
                # 将新位置和路径（旧路径 + 当前方向）加入队列
                q.append(((ny, nx), path + [d]))

# 输出结果：
# 找到路径：222441144222